Why diversification matters for long-term investors? Meet Shannon's Demon
Any introduction to finance will mention that diversification is extremely important. Intuitively, it is easy to understand that diversification reduces risks. If I own stocks in two companies, and one of them goes bankrupt, I lose less than if I had invested all my money in it. However, what appears less intuitive is that diversification itself will increase investment portfolio returns. This phenomenon is known as Shannon’s Demon, from the name of its inventor Claude Shannon, also famous for his work on cryptography.

Let’s take the following scenario: I am an investor who can purchase two assets with completely random and unpredictable returns. My crystal ball is broken, so I cannot know in advance which of the two assets will perform better. They can be modeled by a random walk. Any change to my investment portfolio will cost a 1% transaction fee.
I can use the following two strategies:
- put 100% of my money in one of the two assets and hope it performs well
- put 50% of my money in each asset and rebalance the portfolio every 6 months to keep each position at 50%

I made a Monte-Carlo experiment that simulates the above scenario 100,000 times over 20 years (5040 trading days). After inspecting the final returns, I observed the following:
- in nearly 100% of outcomes, the balanced portfolio beats investing everything in the worst-performing asset
- in 70% of outcomes, the balanced portfolio also beats investing everything in the best-performing asset
Explanation
The second observation might be surprising, but can be easily explained. The trick is that regular rebalancing will create a mechanical way to “buy low and sell high”.
Let’s illustrate it step by step:
- at the start, I own 500 of asset X, for a value of 10$ each, and 500 of Y for the same value
| Name | Price | Position | Value |
|---|---|---|---|
| X | 10$ | 500 | 5,000 |
| Y | 10$ | 500 | 5,000 |
- after 6 months, my position in X experienced explosive growth and now trades at 50$, while Y is stable at 10$
| Name | Price | Position | Value |
|---|---|---|---|
| X | 50$ | 1000 | 25,000 |
| Y | 10$ | 500 | 5,000 |
- I rebalance the portfolio, and now own 15,000$ in X and 15,000$ in Y
| Name | Price | Position | Value |
|---|---|---|---|
| X | 50$ | 300 | 15,000 |
| Y | 10$ | 1,500 | 15,000 |
- 6 months later, X performed poorly and is back at 10$, while Y is now worth 20$
| Name | Price | Position | Value |
|---|---|---|---|
| X | 10$ | 300 | 3,000 |
| Y | 20$ | 1,500 | 30,000 |
- I rebalance, and now own 16,500$ in X and 16,500$ in Y
| Name | Price | Position | Value |
|---|---|---|---|
| X | 10$ | 1,650 | 16,500 |
| Y | 20$ | 825 | 16,500 |
Over the last scenario, my portfolio gained 23,000$. If I had invested everything into Y, I would have gained only 10,000$. And if I had bough and held X over the same time, I would not have made any profit.
Caveat 1: correlated assets
One important thing to consider is that this only work with assets that are not positively correlated. A positive correlation means that both assets will move up at the same time, and down at the same time. In this situation, the balanced portfolio will still perform better than the worst of the two assets, but will most of the time underperform the best-performing asset.
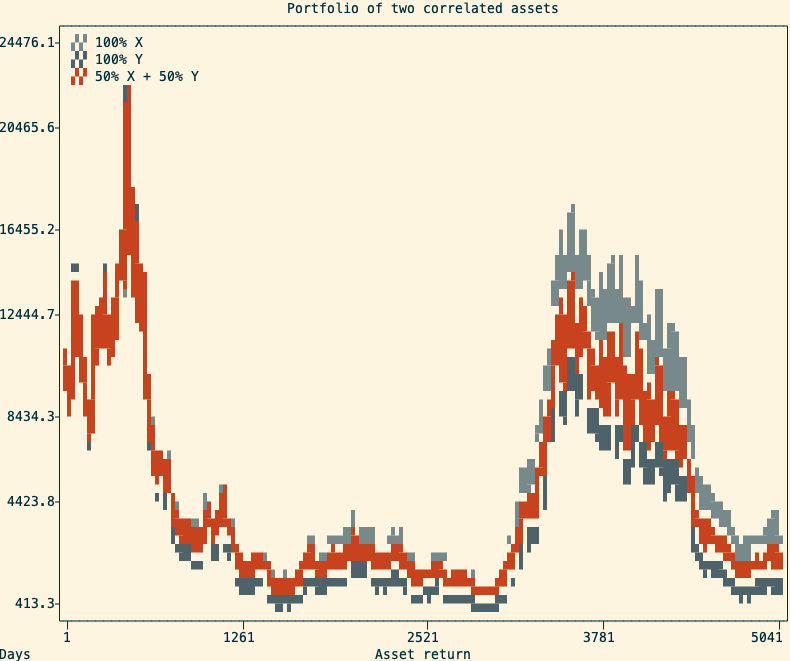
In practice, many asset returns are very correlated with each other. For example, in the stock market, we can observe periods where the large majority of stocks tend to move up (bull markets) or down (bear markets). This makes the creation of a diversified stock portfolio more complicated than just randomly picking multiple stocks to purchase. This is also why it is often advised to diversify across multiple asset classes (ie, stocks, bonds, commodities, and cash).
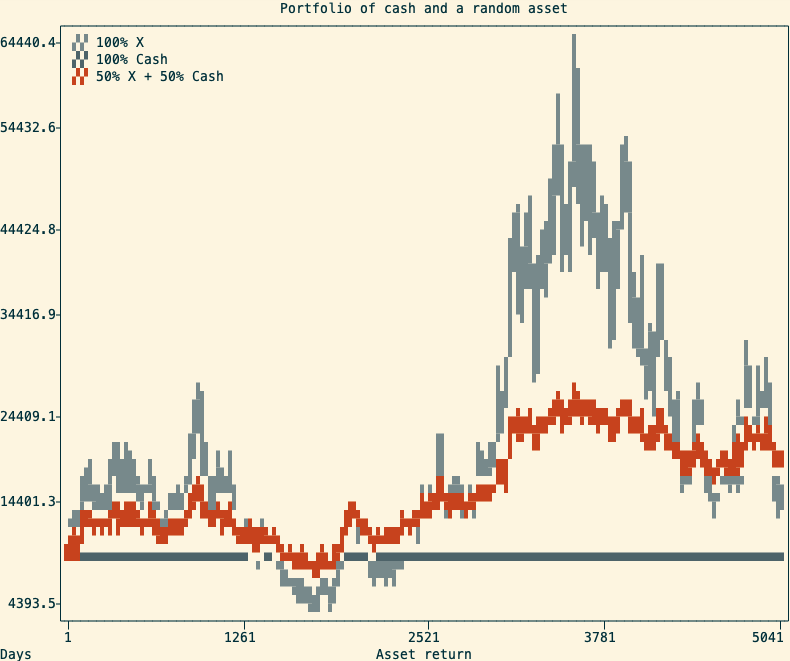
A common way to make use of Shannon’s Demon is to use an asset with a stable price (ie. a money market fund) alongside a volatile one. A portfolio with 50% cash and 50% in a volatile asset will not only cut the risk in half but sometimes outperform being 100% in a single volatile asset. Simulating 10000 random walks over 20 years, in 91% of cases, the balanced portfolio beats investing everything in the random walk.
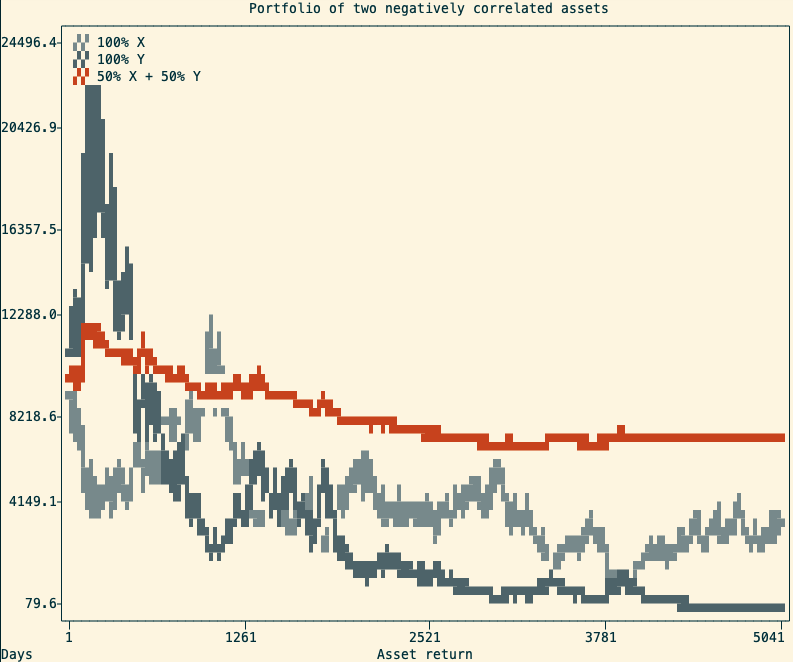
An alternative use of Shannon’s Demon is to profit from negatively correlated positions. This can be done by taking two positively correlated assets and being long on one, and short on the other. This strategy is called pair trading, and it is not something you should try at home.
Caveat 2: real-life is not as simple
Obviously, there’s more to portfolio management than just diversification and rebalancing. First, the 50/50 repartition I used in this article is rarely optimal. The common calculation used for optimal position sizing is the Kelly criterion, which would need an entire article dedicated to it to cover it properly.
In previous examples, I used a fixed 6 months period between rebalances. I chose this period for completely arbitrary reasons. An optimized rebalancing strategy would need to take into account asset variances, investment time-frames, and transaction costs to determine the rebalancing intervals.
Lastly, while simulations using random walks are a useful mathematical tool, they might not reflect real market conditions. A portfolio composed of assets that are likely to depreciate over time is unlikely to be profitable, no matter how diversified it is. This is why asset purchases should be carefully researched, eventually with the help of a professional financial advisor (not me).