Like many block ciphers, AES (Advanced Encryption Standard aka Rijndael) comes with plenty of different modes, all labeled with confusing 3 letters names like ECB, CBC, CTR or CFB. Many developers are told that they shouldn’t use ECB (Electronic Code Book) because it doesn’t provide strong data confidentiality. However, a lot of people will assume that the very popular CBC (Cipher Block Chaining) mode is perfectly fit for all use-cases. Sadly, this is not true, because while providing very good data confidentiality, CBC does not guarantee data integrity.

What is this CBC thing about?

The first thing you need to know before understanding what’s CBC is what’s a block cipher. A block cipher is a function that will take a block of plaintext (the human-readable input) of length n and a key, and use that to produce a block of ciphertext (the encrypted gibberish) of length n. AES is the most popular block cipher around right now, as it is recommended by both NIST and NSA, it operates on 128 bits blocks with keys of 128, 192 or 256 bits.

The problem here is that a function meant to take inputs of 128 bits isn’t going to encrypt a large amount of data in a single call. When confronted with that problem, the intuitive solution is to simply divide your data into multiple 128 bits blocks and simply just call AES with the same key on each one of them.

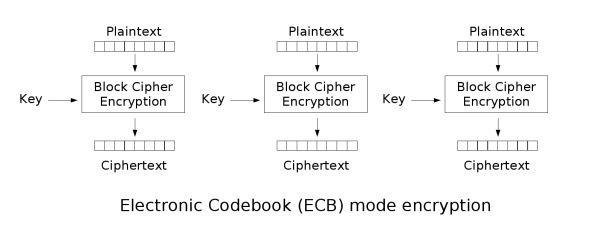
This method is called Electronic Code Book and as I mentioned earlier, is unsafe because data patterns might remain and serve as a basis for analysis. CBC aims to solve this by adding randomness to each call to the block cipher by applying the exclusive-or operation (XOR) to each plaintext block with the previously generated ciphertext block (or a random Initialization Vector (IV), for the first block). Decryption works by doing the process in reverse and XORing each generated plaintext with the previous ciphertext.

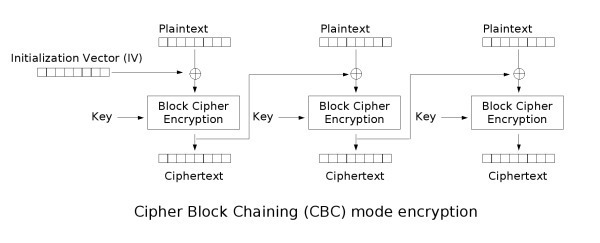
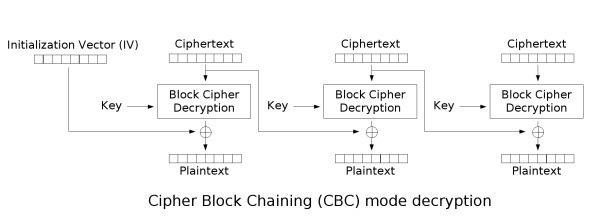
Introducing Bit Flipping attacks

It’s the process of XORing plaintext blocks with the previous ciphertext block during decryption that will introduce a data integrity vulnerability. If we take a look at the XOR truth table, we can see that switching one bit of one of the ciphertext will change the output from 0 to 1, or 1 to 0 :

Ciphertext	Plaintext	Output
0	0	0
1	0	1
0	1	1
1	1	0

What this table is telling us, is that if we switch one bit from the previous block of ciphertext, it will be switched in the next deciphered block too.

Of course, that could cause the previous block of plaintext to be replaced by unpredictable garbage data. Some people could assume that if the ciphertext gets modified, the plaintext will not be anything readable and the application will simply return an error. This is a very dangerous assumption because there are many cases in which some parts of the data might get scrambled yet not trigger any error which could warn the user of an issue and the modified message will affect the system in the way the attacker wants.

Keep in mind that, it’s also possible to alter the first block of data by simply changing the IV, which won’t cause any unpredictable plaintext changes (since the IV is discarded after decryption). This is especially dangerous as sometimes your ciphertext is just a single block.

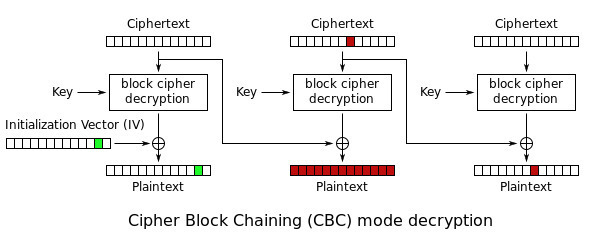
An exploitation scenario

Let’s say Alice wants to send 100$ to Bob through an encrypted banking service. She will first encrypt the ASCII-encoded string “Send 100$ to Bob” with AES-256 and send this order to her banker. This can be done using a simple function like this one (in Go):

func encrypt(plaintext, key []byte) {
	// generate unique IV
	iv := make([]byte, aes.BlockSize)
	io.ReadFull(rand.Reader, iv)

	// instantiate block cipher
	block, _ := aes.NewCipher(key)
	mode := cipher.NewCBCEncrypter(block, iv)

	// encrypt
	ciphertext := make([]byte, len(plaintext))
	mode.CryptBlocks(ciphertext, plaintext)

	fmt.Printf("iv: %x\n", iv)
	fmt.Printf("ciphertext: %x\n", ciphertext)
}

Alice will send by over an insecure channel the following IV and ciphertext:

iv: 9bc423909ac569b5016525cb4b2660b5
ciphertext: c6d55918176051c5a603d62cdf23fa8a

Sadly, this message will get intercepted by Eve. As Eve uses the same banking system as Alice and knows Alice is a good friend of Bob, she can guess the message will be shaped Send xxx$ to Bob. Eve will then simply compute the XOR of Send xxx$ to Bob and Send xxx$ to Eve to know how to change the ciphertext (she doesn’t need to know the actual amount of money being sent). This can be done using this simple function:

func xor(plaintext, malicious []byte) {
	output := make([]byte, len(plaintext))
	for i := 0; i < len(plaintext); i++ {
		output[i] = plaintext[i] ^ malicious[i]
	}

	fmt.Printf("%x\n", output)
}

Which will output:

00000000000000000000000000071907

Since XOR is an associative operation, she can just XOR the previous output with the IV to flip the correct bits. This way, Eve will send back to the banker the altered IV and ciphertext:

iv: 9bc423909ac569b5016525cb4b2179b2
ciphertext: c6d55918176051c5a603d62cdf23fa8a

When the banker decodes them through the decryption function below:

func decrypt(iv, ciphertext, key []byte) {
	// instantiate block cipher
	block, _ := aes.NewCipher(key)
	mode := cipher.NewCBCDecrypter(block, iv)

	// decrypt
	plaintext := make([]byte, len(ciphertext))
	mode.CryptBlocks(plaintext, ciphertext)
	fmt.Printf("plaintext: %s\n", plaintext)
}

It will output:

plaintext: Send 100$ to Eve

What to use instead of CBC?

The safest way to avoid this pitfall is to use authenticated encryption, which ensures data integrity as well as confidentiality. Galois/Counter Mode (GCM) is a popular alternative to CBC that provides authenticated encryption with block ciphers like AES. If you really have no choice and need to use CBC, you can still secure it by computing a message authentication code (MAC) from the ciphertext and IV, this can be done using the popular HMAC algorithm. Although, like with many crypto related topics, message authentication is a tricky subject and would easily require another entire blog post to cover it properly.

Sources and more

Source code for the vulnerable application

Source code for the exploit

Bit Flipping Attack on CBC Mode - Cryptography Stack Exchange

Block cipher mode of operation - Wikipedia

Cryptography I - Coursera