-
Posted on
Managing your Kubernetes cluster using Helm and Terraform
In a previous post, I explained how to manage a Kubernetes cluster with FluxCD. This showed a way to implement a GitOps workflow, which means using a Git repository as the source of truth for the state of your cluster.
Flux introduces multiple new objects in your Kubernetes clusters, and requires using custom software. This makes it harder to adopt by smaller teams without dedicated platform engineers. On the other hand, most teams are already using Terraform. In this article, I will show how to make use of Terraform to manage your kubernetes clusters. This way could be considered GitOps-lite because while changes are kept track of in a Git repository, they are neither enforced nor automatically pulled from the repository.
I will use resources from Google Cloud Platform in the following examples, but everything in this article should be doable in any major cloud platform.

Photo by Geran de Klerk Setting up a cluster with Terraform
First, make sure you have the Terraform CLI installed or download it here. Then, create a new Git repository
mkdir cluster cd cluster git init git remote add origin <your-github-repo>We will then define a basic Google Kubernetes Engine cluster (with two nodes) and indicate Terraform to store the state in a remote Google Cloud Storage bucket, which you will need to create manually. The following HCL should go in the main.tf file:
terraform { required_providers { google = { source = "hashicorp/google" version = "3.5.0" } } backend "gcs" { bucket = "your-unique-tf-state-bucket" prefix = "terraform/state" } } variable "project_id" { description = "project id" } variable "region" { description = "region" } provider "google" { project = var.project_id region = var.region } resource "google_container_cluster" "primary" { name = "${var.project_id}-gke" location = var.region initial_node_count = 2 }This defines the variables “region” and “project_id”, which we pass to the google provider, as those will contain the data relevant to our GCP project. The values of these variables can either be set interactively when running terraform commands or kept in the
terraform.tfvarsfile.You can then proceed to run
terraform initto initialize your project and state. After that, runterraform plan, which will display the changes terraform is about to do, and runterraform applyto apply those changes and create your cluster.Since GKE resources have a state that is a lot more complex than the HCL file above, I suggest using the output of
terraform state show google_container_cluster.primaryto refactor the HCL into a more complete overview of the state. This can in the future avoid unwanted changes to appear in the plans.Authenticating to your cluster
You can now authenticate to your cluster using the Google Cloud CLI. First install it by following the instructions here. Then log into Google Cloud using
gcloud auth login, which should open your browser for a login prompt. After that, usegcloud config set projectto indicate which project you are working on. Finally, rungcloud container clusters get-credentials [YOUR_PROJECT_ID]-gke --zone=[YOUR_REGION]You should now see your cluster appear when you run
kubectl config get-contextsand two nodes should be visible by runningkubectl get nodes.
Photo by Frank Eiffert Installing Helm charts
We will now use the helm terraform provider to install podinfo and set the value
replicaCountto 2. To do this, create a new HCL file, with the following content:provider "helm" { kubernetes { config_path = "~/.kube/config" } } resource "helm_release" "podinfo" { name = "podinfo" repository = "https://stefanprodan.github.io/podinfo" chart = "podinfo" set { name = "replicaCount" value = 2 } }You’ll need to run
terraform init -upgradeto install this new provider. Then you can runterraform planandterraform apply, just like in the previous section.This will act just like
helm upgrade -installand the podinfo release should now appear when runninghelm list. Usingkubectl get podsshould show you two podinfo pods running. You can access the service by runningkubeclt port-forward service/podinfo 9898:9898and thencurl localhost:9898.Going further
Directly applying changes from your local environment doesn’t scale well when multiple people are committing changes to the infrastructure. It also causes safety issues, as changes could be applied locally without having been through a PR review. One way to solve that problem would be to use GitHub Actions to automate planning the changes when a PR is applied and applying when a PR is merged. The SaaS Atlantis can also help solve that problem, as it will act as a GitHub bot that will plan/apply in response to comments.
-
Posted on
A sensible NeoVim configuration
I have been using NeoVim as my main editor for code since 2017. When discussing that with other engineers, a common complaint I hear about (Neo)Vim is that its configuration is overly complicated and confusing. In this post, I will try to address this point by showing simple steps to configure NeoVim into a development capable environment. This should allow you to get essential code editing features (ie. auto-completion, linting, search…) while keeping a minimalist and fast environment.
Installing NeoVim
First of all, install NeoVim by following the instructions on GitHub. Open NeoVim by simply typing
nvimin a terminal.If you want to learn the basics of using vim, type
:Tutor. This will take you to the built-in tutorial.Type the
:CheckHealthcommand into NeoVim’s normal mode, this will tell you if you need to set up anything special.The most important dependency is to have python 3.6+ with the neovim pip package installed as well as node with the neovim npm package. Aside from that, you might need:
- python 2.7 with the neovim package
- ruby with the neovim gem
- perl with the Neovim::Ext module
Once everything is green, let’s go over some basic configurations

Photo by Kenny Eliason Basic configuration
First, you should create your configuration file at
~/.config/nvim/init.vim.To be able to exit NeoVim’s terminal emulator (
:term) by simply pressing escape instead of theCtrl+\ Ctrl+ncombo, add this line to your config file (~/.config/nvim/init.vim):tmap <Esc> <C-\><C-n>mapis the basic operator for mapping keyboard shortcuts.tmapindicates that you want to map these keys in terminal mode only.imapandnmapare respectively for insert and normal mode. As an alternative tomapyou might have to sometimes usenoremapto non-recursively map (this is meant to avoid propagating to mappings you’ve already changed).You’ll also want to be able to switch between windows without having to type a complete command:
nmap <silent> k :wincmd k<CR> nmap <silent> j :wincmd j<CR> nmap <silent> h :wincmd h<CR> nmap <silent> l :wincmd l<CR>These lines will map the switching of commands to
Alt+hjkl. (Note, on mac the only way I’ve managed to configure that was by using the characters output when I press Alt+hjkl on my keyboard).Then, you can do a few tweaks to the appearance. I recommend displaying numbers next to lines, displaying line wrapping, and allowing horizontal scrolling.
set number set nowrap set sidescroll=1You should then add some default tab configurations.
set tabstop=2 set softtabstop=2 set shiftwidth=2 set expandtab set autoindent set fileformat=unixYou also want to be able to override those configurations for each project with a local .nvimrc:
set exrcAnd lastly, this line will allow scripts to run for specific file types:
:filetype plugin onPlugins
Since NeoVim doesn’t have every feature developers usually need out of the box, you will need to be able to install plugins. For that purpose, we will use vim-plug. Installing by runnning:
sh -c 'curl -fLo "${XDG_DATA_HOME:-$HOME/.local/share}"/nvim/site/autoload/plug.vim --create-dirs \ https://raw.githubusercontent.com/junegunn/vim-plug/master/plug.vim'We will then do the first edit to your configuration file
~/.config/nvim/init.vim. Add the following lines to install the plugins you will need:call plug#begin('~/.vim/plugged') Plug 'ctrlpvim/ctrlp.vim' Plug 'tpope/vim-fugitive' Plug 'vim-airline/vim-airline' Plug 'tpope/vim-sleuth' Plug 'neoclide/coc.nvim', {'branch':'release'} call plug#end()Each of the lines starting with
Plugindicates the GitHub repository of a plugin. Save your config file and type:PlugInstallin NeoVim’s normal mode to install them.The plugins this will have installed are the following:
- coc.nvim gives you essential code-editing features like auto-completion using the language server protocol (like VScode)
Ctrlp.vim
Ctrlp.vim is a very efficient file search plugin.
To use it simply press CTRL+P, this will open a file list that you can navigate with arrow keys. Typing any characters will make it search for matching files. You can use CTRL-F and CTRL-B to cycle between the different search modes (files, buffers, or most recently used). CTRL-R will allow you to type in regexes, while CTRL-D will search only in the filenames instead of the full path.
Use the following line to stop this plugin from indexing files outside of your source code:
let g:ctrlp_custom_ignore = '\v[\/](node_modules|target|dist|venv)|(\.(swp|ico|git|svn))$'If you want to integrate more file handling into vim, you can also try NERDTree, which will provide you with a complete file system explorer.
Vim-fugitive
Vim-fugitive is a wrapper around git. It doesn’t require any special configuration to work, as long as you have a git CLI configured on your machine.
It will allow you to use any git command in vim using
:G, you can try it with:G statusto display the result ofgit status. One neat trick is that you can use:G grepto send the result of agit grepdirectly into vim’s quickfix list.Vim-airline
Vim-airline will display the status of your current file as the last line of the editor. It’s basically plug and play and will even automatically detect other plugins you use (like ctrpl or fugitive) and integrate them.
The status line is divided into 6 sections (A, B, C, X, Y, Z) and can be customized with the statusline syntax:
let g:airline_section_b = 'Filetype: %y'
Vim-sleuth
Vim-sleuth aims at automatically adjusting indentation to the file you’re editing. It works by simply overriding the
shiftwidthandexpandtabvariables (which you can set manually in your config file if you want). It doesn’t require any configuration either and generally works pretty well.An alternative to it would be to use editorconfig-vim. This plugin will instead follow the configuration written in a
.editorconfigfile at the root of a project.Coc.nvim
Coc.nvim is really what will give you an IDE-like experience. This plugin will give you auto-complection, linting, and formatting, using language servers protocols. For that part, I recommend using the configuration sample they provide on GitHub. It will give you useful shortcuts to IDE-like features, like
gdto go to a definition,grto list references, and\tfor automatic renaming.
To support every possible language, CoC has its own plugin system. For example,
:CocInstall coc-gowill install the coc-go plugin for the Go programming language and use gopls.Alternatively, NeoVim now has built-in support for LSPs, you can read more about how to configure that in this repo. As this solution still requires to install a few plugins for auto-completion, I consider CoC to be the simplest option around at the moment.
Theming
Of course, everyone loves some colors! Vim and Neovim have a ton of themes that you can example at vimcolorscheme. Each one can be installed with vim-plug like any other plugin. Once it is installed you can use the
colorschemefunction to enable it from your vim config file. For example with the dracula theme:colorscheme draculaConclusion
This post is only scratching the surface of what can be done with NeoVim. As you use this editor more and more, you will probably want to use different configurations, and will probably end up with a few more (or fewer plugins).
-
Posted on
Managing a Kubernetes cluster with Helm and FluxCD
As seen in my previous article, after successfully setting up a Kubernetes Cluster you can install applications on it using the Helm CLI. This is convenient to get started but might not scale well with multiple people administering the cluster.
To make collaboration easier and avoid making mistakes by simply mistyping Helm commands, it is recommended to adopt a GitOps workflow. This consists of using Git to version control the state of the cluster. In this article, I will explain how to use FluxCD to achieve this.

Illustraton by Loik Marras Getting started with FluxCD
First of all, make sure you have a running Kubernetes cluster and have installed kubectl and helm. Then you will need to create a Git repository at your favorite provider (GitHub, Bitbucket, etc…). Once this is done, clone it locally and create a
releasesfolder inside of it. This folder will contain the files defining your Helm releases (a release is an instance of a chart running on a cluster).Let’s start by creating a release for my favorite IRC client, The Lounge. To do this, create a file in
releases/thelounge.yamlcontaining the following data:--- apiVersion: helm.fluxcd.io/v1 kind: HelmRelease metadata: name: thelounge namespace: default annotations: fluxcd.io/automated: "false" fluxcd.io/tag.chart-image: semver:~4.0 spec: releaseName: thelounge chart: repository: https://halkeye.github.io/helm-charts/ name: thelounge version: 4.3.0 values: ingress: enabled: true hosts: - YOUR.OWN.DOMAINThis will be using the chart available on Artifact Hub, and the software will be running on the default namespace, and we ask for an ingress to be created. Don’t forget to commit and push the release!
After creating this repository, you should install FluxCD on your cluster. To do this simply run the following commands:
helm repo add fluxcd https://charts.fluxcd.io kubectl apply -f https://raw.githubusercontent.com/fluxcd/helm-operator/master/deploy/crds.yaml kubectl create ns flux helm upgrade -i flux fluxcd/flux \ --set git.url=git@github.com:[USERNAME]/[REPO] \ --set git.branch=[BRANCH] \ --namespace flux helm upgrade -i helm-operator fluxcd/helm-operator \ --set git.ssh.secretName=flux-git-deploy \ --set helm.versions=v3 \ --namespace fluxYou should now see 3 pods running in the flux namespace:
flux-memcached-869757cb88-77br8 1/1 Running 0 100s flux-59cb4447b9-thpr9 1/1 Running 0 101s helm-operator-686dc669cd-g8kn7 1/1 Running 0 89sFinally, you will need to give read and write access to your git repository to FluxCD. To do this, install fluxctl and run:
fluxctl identity --k8s-fwd-ns fluxThis will print an RSA key that needs to be added as a deploy key to your repository. For GitHub users, go to
https://github.com/YOURUSERNAME/YOURUSER/settings/keys/newto add the key (tick the give write access checkbox).Your release should start getting installed on your cluster soon. You can check the state of your helm releases by running
kubectl get hrIf needed, you can check the FluxCD logs with
kubectl -n flux logs deployment/flux -fIf you want to manually trigger FluxCD to re-read your git repository, use the command:
fluxctl sync --k8s-fwd-ns flux
Illustraton by AbsolutVision Adding your charts
Of course, you might not be able to do exactly what you want using the charts publicly available. FluxCD allows you to add your charts directly through Git.
First, create a
chartsdirectory. Inside this directory, run the following command to create a chart namedmychart:helm create mychartThis will generate a sample chart defining everything that’s required to launch an Nginx server in production. To run this chart, you will have to define a release for it in your
releasesfolder:--- apiVersion: helm.fluxcd.io/v1 kind: HelmRelease metadata: name: myrelease namespace: default annotations: fluxcd.io/automated: "false" fluxcd.io/tag.chart-image: glob:3.1.1-debian-9-* spec: releaseName: myrelease chart: git: ssh://git@github.com/[USER]/[REPO] ref: [BRANCH] path: charts/mychart values: ingress: enabled: true hosts: - host: YOUR.OTHER.DOMAIN paths: ["/"]Like in the previous example, don’t forget to
git commitandgit push. FluxCD will automatically create the new release and you will see a magnificent Nginx welcome page appear at the specified domain.To be able to display something else than the Nginx welcome page, we will give it a configuration file. For this purpose, you can define a configmap in
charts/mychart/templates/configmap.yaml. The following config will redirect every request to a URL of our choice:apiVersion: v1 kind: ConfigMap metadata: name: nginx-conf data: nginx.conf: | events { worker_connections 1024; } http { server { listen 80 default_server; return 301 {{ .Values.redirect }}; } }You will then need to declare the volume by adding this value to
spec.template.specincharts/mychart/templates/deployment.yaml:volumes: - name: nginx-conf configMap: name: nginx-confTo mount the configuration file into the Nginx container, you need to add the following lines to
spec.template.spec.containers[0]in the same file:volumeMounts: - mountPath: /etc/nginx/ readOnly: true name: nginx-confFinally, bump the
versionincharts/mychart/Chart.yaml, and set the redirect URL inreleases/myrelease.yamlby editing the values section like this:values: ingress: enabled: true hosts: - host: YOUR.OTHER.DOMAIN paths: ["/"] redirect: "https://www.youtube.com/watch?v=cFVF26XPcAU"Dive deeper
As this article only really scratches the surface of what Helm and FluxCD can do, I recommend you to also check out the official FluxCD docs and their example repository, as well as the Helm Chart Template Developer’s Guide.
The source code for the examples shown in this article is available on GitHub.
-
Posted on
Self-Hosted Kubernetes with k3s
Kubernetes has been the center of attention of the DevOps community for a few years now. Yet many people find it too daunting to try it out for personal uses. Running a single-node Kubernetes cluster for self-hosting is however not that complicated. In this article, I will show you how to create this using k3s which is a lightweight distribution of Kube.
Preparing the server
Before launching anything Kube related, you might want to make sure the access to your server is secured. Follow this guide for instructions on how to disable root login and enable public-key authentication if it’s not already the case.
I have encountered issues running k3s with the newer version of iptables (nftables) which comes enabled by default on many distributions (like Debian 10). You can check whether or not you’re using nftables with
sudo iptables --version. You should switch back to the legacy iptables by executing:sudo update-alternatives --set iptables /usr/sbin/iptables-legacy sudo rebootIt’s also a good idea to set-up basic firewall rules to filter incoming traffic. I apply these rules for the eth0 interface which handles my server’s internet connection (find yours using
ip a):sudo iptables -A INPUT -i eth0 -p tcp --dport 22 -j ACCEPT # Allow SSH sudo iptables -A INPUT -i eth0 -p tcp --dport 6443 -j ACCEPT # Allow kube API sudo iptables -A INPUT -i eth0 -p tcp --dport 10250 -j ACCEPT # Allow kube metrics sudo iptables -A INPUT -i eth0 -p icmp --icmp-type 8 -j ACCEPT # Allow ping sudo iptables -A INPUT -i eth0 -m state --state ESTABLISHED,RELATED -j ACCEPT # Allow responses to our requests sudo iptables -A INPUT -i eth0 -j DROP # Drop every other incoming packetsDon’t worry about opening ports specific to the applications you want to run in your cluster since k3s will handle it directly. To persist your iptables rules after a reboot, I use the
iptables-persistentpackage.sudo apt install iptables-persistent sudo iptables-save | sudo tee -a /etc/iptables/rules.v4
Illustraton by Taylor Vick Installing k3s
The shell script located at https://get.k3s.io is meant to install k3s automatically. You can directly execute it by running:
curl -sfL https://get.k3s.io | sh -You can check that the service is running by doing
sudo service k3s statusYou can already run basic kubectl commands from your server’s shell. We can check that everything is up and running with the
cluster-infocommand.sudo k3s kubectl cluster-info #Kubernetes master is running at https://127.0.0.1:6443 #CoreDNS is running at https://127.0.0.1:6443/api/v1/namespaces/kube-system/services/kube-dns:dns/proxy #Metrics-server is running at https://127.0.0.1:6443/api/v1/namespaces/kube-system/services/https:metrics-server:/proxy #To further debug and diagnose cluster problems, use 'kubectl cluster-info dump'.Use kubectl and helm
Now you will probably want to use kubectl to control your cluster without being logged in to your server. You will find the instructions on how to install kubectl on your local machine here To do this, you can find the configuration used by k3s at
/etc/rancher/k3s/k3s.yaml, copy it to~/.kube/config. Alternatively, you can pass the config to kubectl with the--kubeconfigoption. You will need to change the server IP in this configuration from127.0.0.1to your server’s external IP address.Now run the
kubectl cluster-infocommand locally and you should see results similar to what you had on your server. A few useful kubectl commands to keep in mind are:kubectl get pods-> list the running podskubectl top nodes-> show the used resources on your nodeskubectl logs [pod_id]-> show the stdout of a pod
To make the installation of software easier on your cluster, helm will act as a package manager. Install helm on your local machine by following these instructions or just run this if you’re on Linux and trust their install script:
curl https://raw.githubusercontent.com/helm/helm/master/scripts/get-helm-3 | bashHelm’s packages are called charts, they are a set of templates defining how to run specific software in Kubernetes. You can now start looking at the available charts in the Helm Hub or with the built-in command
helm search hub [name]. For example, if you want to install The Lounge (a very good self-hosted IRC client/bouncer). You will first need to add the repo that contains its chart:helm repo add halkeye https://halkeye.github.io/helm-charts/Running
helm installwill then be enough to setup Thelounge. Since you might want to access it through a specific domain, we will also ask helm to set up an ingress for it, by giving it additional options to the chart. This gives us the full command:helm install thelounge halkeye/thelounge --version 4.0.6 --set ingress.enabled=true --set ingress.hosts.0="my.domain.com"Your cluster should now be ready for any software you want to run. In a next article, I will explain how you can make better use of helm to keep track of the applications you host.
-
Posted on
Low Tech Crypto : ThreeBallot
Previously in this blog, I have mentioned that cryptographers designed algorithms allowing us to conceal messages without the use of a computer, like Solitaire. Although message privacy is the first subject that comes into everyone’s mind when talking about cryptography, it has many other applications, one of them being the design of secure voting systems. In this post, I will talk about ThreeBallot voting system, a system designed by Ronald Rivest (the R in RSA) which aims at creating a secure voting protocol entirely based (almost entirely) on paper ballots.

Photo by Arnaud Jaegers End-to-end auditable voting systems
Before we start taking a look at ThreeBallot, we need to summarize the objectives of cryptographic voting systems. In general, cryptographic voting systems aims at being end-to-end auditable, which means two things:
- Anyone can proceed to a recount
- Every voter has a way to know if their vote was counted
This second property is usually achieved by giving a receipt of its vote to the voter. However, this receipt should not contain enough information to allow an attacker to breach the privacy of the vote, as each vote must remain secret to avoid vote-buying or coercion.
Introducing the multi-ballot
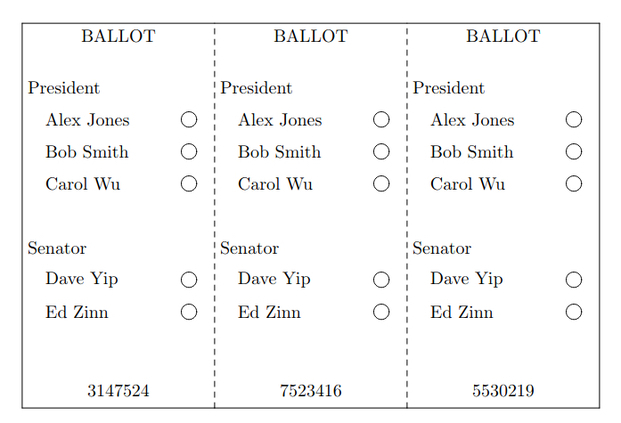
A sample ThreeBallot multi-ballot The ThreeBallot system aims at solving this problem with the use of a “multi-ballot”. The multi-ballot is a voting ballot that can be split into 3 parts (one per column), all containing the list of candidates (one per row) with optical-scan checkboxes as well as a unique identifier. To vote, simply check 2 boxes on the row of the candidate you want to vote for, and 1 box on the row of each candidate you want to vote against. A ballot will be considered spoilt if all three boxes for a candidate are checked, or none for another candidate.

A sample filled ThreeBallot multi-ballot The validity of the ballot will need to be checked (by machine) before being split into 3 separate ballots. The voter will then chose which parts of the ballot to be used as a receipt and receive a printed copy of it, before casting the 3 ballots.

A single ballot, used as receipt When the election is complete, every ballot is displayed publicly. Anyone can proceed to a count, the results are inflated by the number of voters (one box as to be checked minimum) but the difference between candidates will remain the same. The voters can each check that their ballot appears with the correct vote and ballot ID, or contest the vote using their receipt. The voters cannot use their receipt as a proof of having voted for a candidate, as you need at least 2 of the 3 ballots to tell that, thus maintaining vote secrecy.
Limitations
Despite looking very good on paper, this voting system sadly has many practical vulnerabilities. First of all, despite being paper-based it still requires a machine to print ballots with unique identifiers, and another one to check the validity of the ballots before casting them. Both of these machines represent weak points of the system, as one of them failing would stop the election from taking place correctly. A single malfunction of the checker machine would also be enough to make the entire election null because the system doesn’t provide any way of spoiling a vote after it’s cast. Privacy breaches could also happen if these machines were to be compromised, as an attacker could record which identifiers are part of the same multi-ballot and use it to connect receipts to a full ballot.
In a follow up paper, Charlie Strauss points out that voter coercion can still happen with methods as simple as asking the voter to take a picture of their ballot using a smartphone. According to Strauss, it would also be trivial to double or triple vote by modifying the ballot after having validated it and before casting it. Voters might also give away their receipts or simply throw them in the nearest trash can, making their vote non-auditable and giving an attacker the opportunity of changing them.
In a second paper, Strauss also points out the cryptographic weakness of ThreeBallot. Since one part of the multi-ballot restricts choice on the two other parts (a candidate can’t be entirely blank or checked), the receipt is leaking information about the actual vote. Combining this information with voter bias (ie. party preference), and the publicly displayed ballots, it becomes statistically possible to link a receipt with its two other ballot parts. This is especially concerning in a situation where the attacker could coerce the voter into not only voting for a specific candidate but also checking a specific pattern on its ballot.
Legacy
Many improvements to the ThreeBallot voting system have been suggested, but as with many security protocols, improving security often comes with useability issues. This led to the slow abandonment of this protocol. However, the insights gained through ThreeBallot later allowed the creations of new secure voting systems, such as Scantegrity, which was used in actual elections by the city of Takoma Park, in 2009 and 2011.
subscribe via RSS